Note: Currency and terminology may differ depending on your region.
Watch Video
Please read
FramR calculates both labour and materials into the frame cost. This means the frame cost is higher than if just calculating materials as the cost, giving an accurate
and true cost of making the frame.
Markups are therefore applied as a net markup which may look much smaller than you are used to. Net markups reflect the true amount of profit
you return from making your frames.
More information about markups?
Labour can be turned off by setting your hourly rate to zero, and a Gross markup applied if you wish.
Frames come in many various sizes and complexities, and it's often the case that a smaller frame or framing material may cost the same or even more than a larger one.
We all know it's much easier to sell a larger frame or framing material to the customer at a higher price, even if it does cost the same or less than the smaller size.
FramR solves this with accuracy and ease by giving the ability to apply different markups on smaller and larger frames.
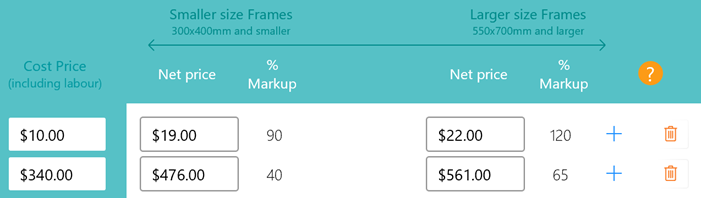
Firstly enter a low cost into the cost column, (Note; the cost price includes labour).
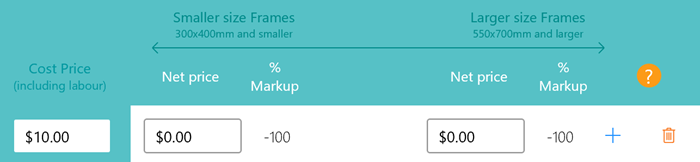
In the next column enter your preferred selling price (before sales tax, if applicable). A % markup will be displayed, this is the % markup that will be applied to any frames 300x400mm or smaller.
It is also the minimum % markup that will be applied to any items that cost less than the cost price entered.

Then enter a selling price for the larger size. Again a % markup will be displayed, this is the maximum % markup to be applied to any frames 550x700 or larger. It is also the maximum % markup applied to lower cost items.
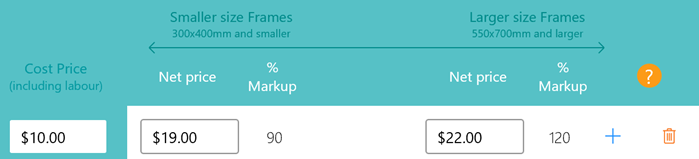
Markups will be applied on a smooth sliding scale to frames sizes between those two inputed sizes.
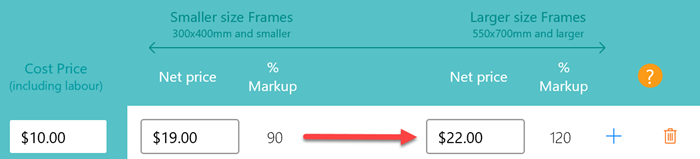
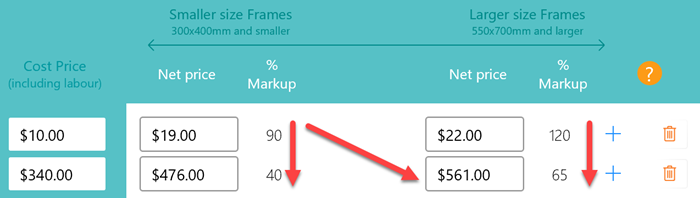
It's often the case in retail that a higher cost item will have a lower markup applied. That same rule generally applies to framing. Even though we are applying a higher markup to larger frames, a frame the same size that cost more may need to have a smaller markup applied
to make it affordable to the customer.
In the next step we'll show you how that is acheived.
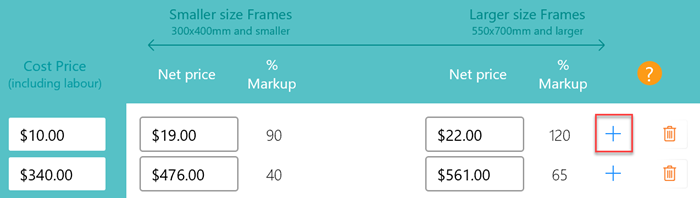
Click on the Plus button to add a new row.
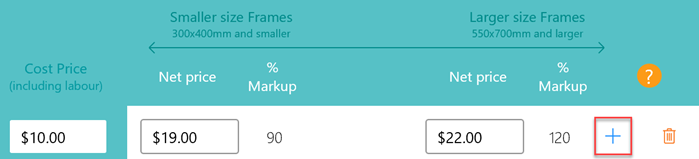
Enter a new cost price, then enter your selling price for the small size. This is the minimum calculated % markup applied to any small frames costing at and above your entered cost price.
Also enter the selling price for your large size. The calculated markup is the minimum that will be applied to any large frames costing at and above your entered cost price.
Markups can be setup with only two cost points so that markups increase on a smooth sliding scale between those two cost and size points.
If you wish, other price points can also be entered to have greater control over your selling price at various costs.
Tip
To find out what your most popular frames cost; price them up on the Job form and look at the price breakdown to see the total cost. Remember that cost is both labour and materials.
Click on the plus button on the row where you want the next row to appear below.
Enter your cost and selling prices same as before.
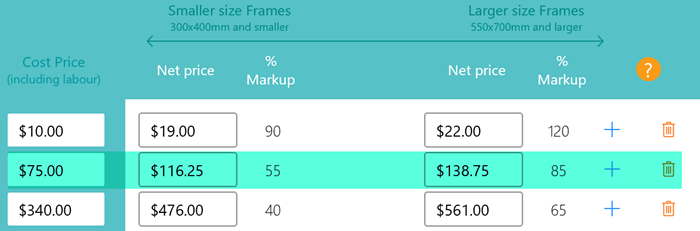
Markups are smoothly increased between each cost and size point, to ensure that there are no sudden, awkward price jumps.
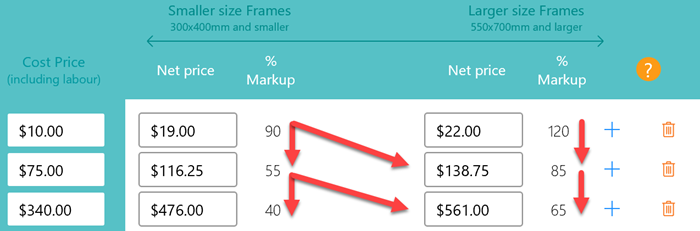
About the two size points
Our price modelling over the past 20 years has shown that there are two critical sizes when it comes to setting minimum and maximum markups.
It can be difficult to apply a higher markup on frames under 0.12 square metres (around 300x400mm) due to the high cost of making the frame.
It's much easier to apply the greatest markup to anything over 0.38 square metres (around 550x700mm) due to the fact that although the cost may not have increased, the customer perception of worth has.
In the model below you can see that the maximum and minimum prices have been applied, and that any frame sizes that fall between those two sizes will have their markup applied proportionally on a smooth sliding scale.
For example; we can see that a frame/material with a square metre size of 0.25sqm (around 450x550mm), half way between 0.12sqm and 0.38sqm will have a % markup of around 62% (half way between 30% and 90%) giving a net selling price of $12.96.












